Konveks? Konkav? Kon-kva?
Det hender ein støyter på ord ein trudde ein visste kva tyder, men der det ser ut til av samanhengen at andre forstår noko anna enn deg.
AV SIGBJØRN HJELMBREKKE
Eit døme på at ord kan oppfattast på fleire måtar, er ordparet positivt/negativt. Oftast tenkjer ein at noko som er positivt, er bra, medan noko negativt er dårleg. Men om legen seier at testresultatet ditt er positivt, er det truleg negativt.
Eit anna døme er adjektivet varm. Omnar kan vera varme. Ord kan også vera varme. Er det same typen varme? Og kva slags varme er det i varme fargar? Tydinga av ordet er kontekstuell.
 Eit interessant døme såg me i Kvitt eller dobbelt for ei tid sidan. Ein som var oppe i norske kommunevåpen, snakka om høgre sida av våpenskjoldet der andre ville ha sagt venstre. Han forklarte at han snakka om heraldisk høgre. I dette ligg at høgre er det som er til høgre for den som held skjoldet. Den som ser på skjoldet, vil oppfatte den same sida som venstre. Kva ein forstår som høgre eller venstre, er altso avhengig av perspektivet.
Eit interessant døme såg me i Kvitt eller dobbelt for ei tid sidan. Ein som var oppe i norske kommunevåpen, snakka om høgre sida av våpenskjoldet der andre ville ha sagt venstre. Han forklarte at han snakka om heraldisk høgre. I dette ligg at høgre er det som er til høgre for den som held skjoldet. Den som ser på skjoldet, vil oppfatte den same sida som venstre. Kva ein forstår som høgre eller venstre, er altso avhengig av perspektivet.
Bakgrunnen for denne teksten er ei tid då eg sleit med å sjå samanhengen mellom tydingar. Det handlar, som det går fram av tittelen, om ordparet konveks/konkav.
Barnelærdom mot universitetslærdom
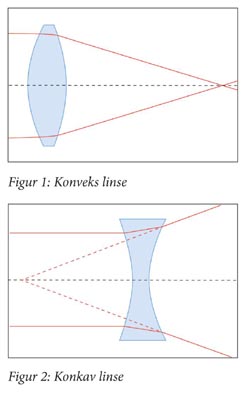
På barneskulen lærte eg om konkave og konvekse linser. Konkave linser kavar seg innover på midten og spreier lyset. Konvekse linser veks på midten og samlar lyset.
 Som student i samfunnsøkonomi møtte eg orda konveks og konkav på nytt. Det har seg nemleg slik at økonomar, matematikarar og dilikt likar å snakka om konvekse og konkave kurver og funksjonar.
Som student i samfunnsøkonomi møtte eg orda konveks og konkav på nytt. Det har seg nemleg slik at økonomar, matematikarar og dilikt likar å snakka om konvekse og konkave kurver og funksjonar.
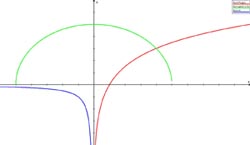
Den konvekse kurva «heng» på midten. 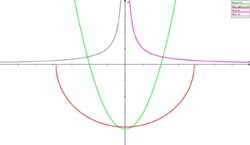 Midten ligg altso nedanfor ei rett line mellom ytterpunkta. Omvendt bøyer den konkave kurva seg oppover på midten. Alle kurvene i figur 3 er konkave. Alle i figur 4 er konvekse.
Midten ligg altso nedanfor ei rett line mellom ytterpunkta. Omvendt bøyer den konkave kurva seg oppover på midten. Alle kurvene i figur 3 er konkave. Alle i figur 4 er konvekse.
Koplinga mellom linsene frå barneskulen og kurvene frå universitetet er ikkje heilt innlysande. Kva gjer ei konveks kurve konveks?
Kva seier ordbøkene?
Nynorskordboka seier:
konkav (frå lat.) bogen, krumma innover; innhol, skålforma; mots konveks / ei k- linse konkavlinse ~itet m1 det å vere konkav ~linse spreielinse
konveks (lat. ’kvelvd’) bogen, krumma utover; kuven; mots konkav / ei k- linse konvekslinse ~itet det å vere konveks ~linse samlelinse
So noko konkavt er skålforma, medan noko konvekst er kvelvd. Dette passar med barnelærdomen, men ikkje med matematikken. Kva er ei konveks kurve? Ho liknar då meir på ei skål enn på det kvelvde taket i ei kyrkje?
Online Etymology Dictionary skriv:
concave from L. concavus «hollow,» from com- intensive prefix + cavus «hollow» (see cave (n.)).
convex from M.Fr. convexe, from L. convexus «vaulted, arched,» pp. of convehere «to bring together,» from com- «together» + vehere «to bring» (see vehicle). Possibly from the idea of vaults carried together to meet at the point of a roof.
Definisjonen liknar altso definisjonen i Nynorskordboka. Ordbøker kan ikkje hjelpa oss med å forstå korleis ordboksdefinisjonane heng saman med bruken i matematikken.
Kva seier matematikkboka?
Matematikkbøkene Knut Sydsæter har skrive for samfunnsøkonomar, nyttar omgrepa konveks og konkav mykje. Forfattaren definerer (sagt med mine ord) konkave funksjonar som slike som går mindre oppover (eller meir nedover) di lenger til høgre ein kjem i figuren. Dei konvekse går brattare og brattare oppover, dvs. mindre og mindre nedover. Ein konveks funksjon gjev ei kurve med alle tangentar på undersida, medan ei konkav kurve er ei med tangentane på oversida.
Ifylgje ordboka skal noko konvekst krumma utover. På kva måte krummar dei konvekse kurvene utover? Kva forfattaren av matematikkboka enn tenkjer om dette, gjer han ingenting for å knyta den matematiske forståinga av omgrepa konveks/konkav til den kvardagslege og opphavlege.
Kva seier Internett?
I ein artikkel i filosofitidsskriftet Mind skreiv E. Williams i 1971:
For ᴖ we are inclined to use the general term convex, and no difficulty is felt in using the specific terms: arched, raised, humped […]. Conversely, for ᴗ, we are inclined to use the general term concave and the specific terms: dished, sagged, recessed, sunk […]. We do not ordinarily apply, e.g. dished to ᴖ nor, e.g. domed to ᴗ.
Det ser altso ut til at matematikarar og økonomar har ei forståing av konveks og konkav som, i det minste i si enklaste form, er motsett av den folk flest har.
Elles har Internett mangt å seia om andre geometriske forståingar av omgrepa. Ein figur er konveks dersom alle par av punkt på figuren kan knytast saman med ein rett strek som er fullstendig innanfor figuren. Ein kube, ei kule og ein pyramide er alle konvekse, men alt som har ei grop eller eit hakk i seg, er ikkje-konvekst og blir stundom kalla konkavt. Eit polygon (ein mangekant) er konkavt dersom ein indre vinkel er større enn 180 grader, altso dersom ei rett line gjennom figuren kan dela han i meir enn to delar. Dette heng saman med forma på linsene. Men kurvene?
Ein kuppel – kon-kva?
 Ein kuppel er konveks sett frå utsida. Alle punkt på kuppelen kan knytast saman med ei rett line som ligg innanfor kuppelen.
Ein kuppel er konveks sett frå utsida. Alle punkt på kuppelen kan knytast saman med ei rett line som ligg innanfor kuppelen.
Innsida er konkav ettersom punkt i taket må knytast saman med ei line som går tvers gjennom rommet. Kva er kuppelen? Rett svar er nettopp at han er konveks oppover og konkav nedover. Konveks oppover og konkav nedover er altso det same. For å forvirra vidare er det oftast det same som konveks nedanfrå og konkav ovanfrå. Når me les om konkave funksjonar i matematikkboka, er det snakk om konkavitet ovanfrå og nedover. Dette er den vanlege forståinga i matematikken. Når matematikkboka mi fortel om slike kuppelforma grafar, seier ho at den hole sida skal vera ned. Forfattarane kunne ha sagt at den konkave sida skal vera ned og den konvekse opp. Det gjer dei ikkje, truleg av frykt for å forvirra oss.
Konkav:
konkav nedover
konveks oppover
konkav ovanfrå (og ned)
konveks nedanfrå (og opp)
 Konveks:
Konveks:
konveks nedover
konkav oppover
konveks ovanfrå
konkav nedanfrå
Denne problemstillinga liknar altso på den me nemnde innleiingsvis, om heraldisk høgre. Det som er høgre for den som held skjoldet, er venstre for den som ser på skjoldet. Det er eit spørsmål om perspektiv.
Avsluttande strøtankar
Dimed kan det sjå ut til at me er i mål! Grunnen til at ein omtalar konvekse kurver som konvekse, er altso ikkje at dei er konvekse i nokon absolutt forstand, slik som konvekse linser, mengder og polygon. Dei er konvekse berre i eit implisitt perspektiv, nemleg ovanfrå.
Oi! Men vent no litt! I 1941 skreiv den namngjetne økonomen Adolf Kozlik:
Terminology (b) [concave/convex downward/upward] is ambiguous because it is not clear without further specification whether the terminology means that the convex side of the curve looks upward or downward or that the curve appears to be convex or concave as the observer looks upward or downward.
Det som er vanleg, er det fyrste, at det er den konvekse sida av kurva som «ser» oppover. Lat oss kalla det «heraldisk oppover»! Konveksitet og konkavitet er utruleg vanskeleg å snakka om utan gjennom konkrete definisjonar som alle er samde om. Kozlik igjen:
Although nomenclature is a matter of convention and taste […] a uniform language has great advantages. It may therefore, be recommended to standardize the terminology concerning the shape of curves.
Innhaldet i orda konveks og konkav er difor avhengig av samanhengen, dvs. av kva som er konvekst eller konkavt. Dersom det er snakk om kurver eller funksjonar, er innhaldet i tillegg avhengig av perspektiv. Heldigvis har Kozlik fått viljen sin. Når ikkje anna er nemnt, er perspektivet standardisert til «heraldisk ovanfrå»!
-- Sigbjørn Hjelmbrekke er samfunnsøkonom og forskar ved Telemarks-forsking.

